Improvements of Framework:

In this project, I did some optimizations for my framework to better fit the requirements. The first improvement is add a RGBA32 format color attachment so that I can render the depth data in fragment shader with high precision. The second improvement is change the clear values of color attachments from black to white so that the depth value will be 1 if no geometry is draw on the pixel. One last improvement I made which is not related with this project is switching rendering model from blinn-phong to GGX BRDF.

Implementations:

Shadow Map Rendering:

In the shadow pass, Instead of drawing nothing to color attachment and using depth frame buffer directly for shadow mapping, I render the depth value z, together with 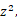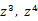into on RGBA32_SFLOAT color attachment:

Rendered depth image

RGBA channels of depth buffer, representing 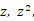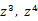respectively.

Blur Implementation:

In order to make gaussian blur, I followed the separate filter strategy and split horizontal and vertical blur into two compute shaders. In the first shader, the horizontal filter is performed based on original depth texture and write into a staging texture of same size. In the horizontal filtered depth will be retrieved from staging texture and write back to original depth texture after performing a vertical filter. At first, I tried to done both filter in one single shader but it seems to be not work well because it requires both read and write operations on same texture, which leads to dirty results even with barrier synchronization and volatile declarations.

Original depth buffer

After horizontal blur

After vertical blur

A Pitfall of Cholesky Decomposition

When the shadow depth value is one, the f tern of Cholesky Decomposition algorithm will likely be zero, and hence results in nan or inf values of c1, c2, c3. These bad return values are likely to give weird shadow results if not handled correctly. My suggestion is to judge if the delta value of equation 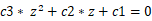(i.e. )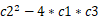
is larger than zero then do the Hamburger 4MSM algorithm, else return s=1, rather than judge if delta is smaller or equal to zero then return s=1, else do the Hamburger algorithm. Since a nan delta is neither larger nor smaller than zero and in the former solution, bad deltas will simply escape MSM calculation and return ones.

MSM implemented with the latter solution returns weird results.

Artifacts

Two artifacts are found after the implementation of MSM. One is light leaking of overlapped shadows and the other is some shadows appears to have layered effect.

Light leaking

Layered shadow

Results With Different Blur Widths

Width: 1

Width: 4

Width: 15

Width: 35